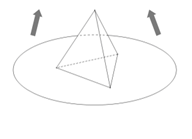
(本小题满分14分)某商场为促销要准备一些正三棱锥形状的装饰品,用半径为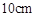 的圆形包装纸包装.要求如下:正三棱锥的底面中心与包装纸的圆心重合,包装纸不能裁剪,沿底边向上翻折,其边缘恰好达到三棱锥的顶点,如图所示.设正三棱锥的底面边长为
的圆形包装纸包装.要求如下:正三棱锥的底面中心与包装纸的圆心重合,包装纸不能裁剪,沿底边向上翻折,其边缘恰好达到三棱锥的顶点,如图所示.设正三棱锥的底面边长为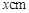 ,体积为
,体积为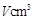 .
.
(1)求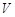 关于
关于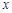 的函数关系式;
的函数关系式;
(2)在所有能用这种包装纸包装的正三棱锥装饰品中,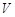 的最大值是多少?并求此时
的最大值是多少?并求此时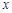 的值.
的值.
相关知识点
推荐套卷
(本小题满分14分)某商场为促销要准备一些正三棱锥形状的装饰品,用半径为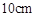 的圆形包装纸包装.要求如下:正三棱锥的底面中心与包装纸的圆心重合,包装纸不能裁剪,沿底边向上翻折,其边缘恰好达到三棱锥的顶点,如图所示.设正三棱锥的底面边长为
的圆形包装纸包装.要求如下:正三棱锥的底面中心与包装纸的圆心重合,包装纸不能裁剪,沿底边向上翻折,其边缘恰好达到三棱锥的顶点,如图所示.设正三棱锥的底面边长为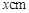 ,体积为
,体积为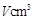 .
.
(1)求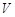 关于
关于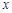 的函数关系式;
的函数关系式;
(2)在所有能用这种包装纸包装的正三棱锥装饰品中,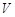 的最大值是多少?并求此时
的最大值是多少?并求此时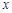 的值.
的值.