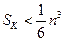一辆邮政车自A城驶往B城,沿途有n个车站(包括起点站A和终点站B),每停靠一站便要卸下前面各站发往该站的邮袋各一个,同时又要装上该站发往后面各站的邮袋各一个,设该车从各站出发时邮政车内的邮袋数构成一个有穷数列 ,
,
试求:(1)
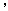
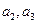
(2)邮政车从第k站出发时,车内共有邮袋数是多少个?
(3)求数列 的前k项和
的前k项和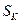 并证明:
并证明: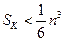
推荐套卷
一辆邮政车自A城驶往B城,沿途有n个车站(包括起点站A和终点站B),每停靠一站便要卸下前面各站发往该站的邮袋各一个,同时又要装上该站发往后面各站的邮袋各一个,设该车从各站出发时邮政车内的邮袋数构成一个有穷数列 ,
,
试求:(1)
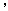
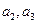
(2)邮政车从第k站出发时,车内共有邮袋数是多少个?
(3)求数列 的前k项和
的前k项和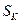 并证明:
并证明: