为了解某校九年级学生体育测试成绩情况,现从中随机抽取部分学生的体育成绩统计如下,其中右侧扇形统计图中的圆心角α为36°.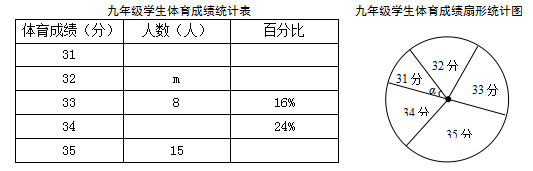
根据上面提供的信息,回答下列问题:
(1)m= ;抽取部分学生体育成绩的中位数为 分;
(2)已知该校九年级共有500名学生,如果体育成绩达33分以上(含33分)为优秀,请估计该校九年级学生体育成绩达到优秀的总人数.
相关知识点
推荐套卷
为了解某校九年级学生体育测试成绩情况,现从中随机抽取部分学生的体育成绩统计如下,其中右侧扇形统计图中的圆心角α为36°.
根据上面提供的信息,回答下列问题:
(1)m= ;抽取部分学生体育成绩的中位数为 分;
(2)已知该校九年级共有500名学生,如果体育成绩达33分以上(含33分)为优秀,请估计该校九年级学生体育成绩达到优秀的总人数.