(本小题满分12分)如图,曲线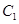 是以原点
是以原点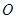 为中心,
为中心,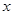 轴上的点
轴上的点 为焦点的椭圆,曲线
为焦点的椭圆,曲线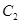 是以原点
是以原点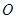 为顶点,
为顶点,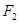 为焦点的抛物线的一部分(
为焦点的抛物线的一部分( ),
), 是曲线
是曲线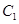 和
和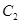 的交点,已知
的交点,已知 为钝角且
为钝角且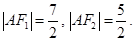

(Ⅰ)分别求曲线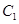 和曲线
和曲线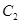 的方程;
的方程;
(Ⅱ)过点 作倾斜角互补的两条直线,分别交曲线
作倾斜角互补的两条直线,分别交曲线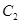 于
于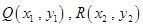 ,求
,求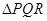 面积的最大值.
面积的最大值.
相关知识点
推荐套卷
(本小题满分12分)如图,曲线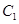 是以原点
是以原点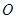 为中心,
为中心,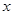 轴上的点
轴上的点 为焦点的椭圆,曲线
为焦点的椭圆,曲线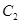 是以原点
是以原点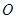 为顶点,
为顶点,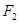 为焦点的抛物线的一部分(
为焦点的抛物线的一部分( ),
), 是曲线
是曲线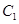 和
和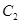 的交点,已知
的交点,已知 为钝角且
为钝角且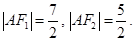

(Ⅰ)分别求曲线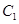 和曲线
和曲线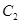 的方程;
的方程;
(Ⅱ)过点 作倾斜角互补的两条直线,分别交曲线
作倾斜角互补的两条直线,分别交曲线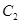 于
于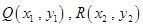 ,求
,求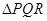 面积的最大值.
面积的最大值.