(本小题满分10分)如图,已知点 ,直线
,直线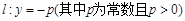 ,
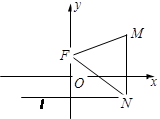
, 为平面内的动点,过
为平面内的动点,过 作
作 的垂线,垂足为
的垂线,垂足为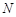 ,且
,且 .
.
(1)求动点 的轨迹
的轨迹 的方程;
的方程;
(2)设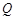 是
是 上的任意一点,过
上的任意一点,过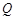 作轨迹
作轨迹 的切线,切点为
的切线,切点为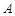 、
、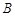 .
.
①求证: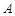 、
、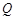 、
、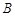 三点的横坐标成等差数列;
三点的横坐标成等差数列;
②若 ,
,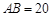 ,求
,求 的值.
的值.
推荐套卷
(本小题满分10分)如图,已知点 ,直线
,直线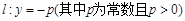 ,
, 为平面内的动点,过
为平面内的动点,过 作
作 的垂线,垂足为
的垂线,垂足为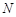 ,且
,且 .
.
(1)求动点 的轨迹
的轨迹 的方程;
的方程;
(2)设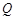 是
是 上的任意一点,过
上的任意一点,过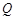 作轨迹
作轨迹 的切线,切点为
的切线,切点为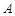 、
、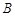 .
.
①求证: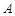 、
、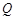 、
、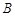 三点的横坐标成等差数列;
三点的横坐标成等差数列;
②若 ,
,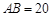 ,求
,求 的值.
的值.