(本小题满分13分)某普通高中共有 个班,每班
个班,每班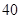 名学生,每名学生都有且只有一部手机,为了解 该校学生对
名学生,每名学生都有且只有一部手机,为了解 该校学生对 两种品牌手机的持有率及满意度情况,校学生会随机抽取了该校
两种品牌手机的持有率及满意度情况,校学生会随机抽取了该校 个班的学生进行统计, 得到每班持有两种品牌手机人数的茎叶图以及这些学生对自己所持手机的满意度统计表如下:
个班的学生进行统计, 得到每班持有两种品牌手机人数的茎叶图以及这些学生对自己所持手机的满意度统计表如下:

(Ⅰ)随机选取1名该校学生,估计该生持有 品牌手机的概率;
品牌手机的概率;
(Ⅱ)随机选取1名该校学生,估计该生持有 或
或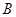 品牌手机且感到满意的概率;
品牌手机且感到满意的概率;
(Ⅲ) 两种品牌的手机哪种市场前景更好?(直接写出结果,不必证明)
两种品牌的手机哪种市场前景更好?(直接写出结果,不必证明)
推荐套卷
(本小题满分13分)某普通高中共有 个班,每班
个班,每班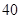 名学生,每名学生都有且只有一部手机,为了解 该校学生对
名学生,每名学生都有且只有一部手机,为了解 该校学生对 两种品牌手机的持有率及满意度情况,校学生会随机抽取了该校
两种品牌手机的持有率及满意度情况,校学生会随机抽取了该校 个班的学生进行统计, 得到每班持有两种品牌手机人数的茎叶图以及这些学生对自己所持手机的满意度统计表如下:
个班的学生进行统计, 得到每班持有两种品牌手机人数的茎叶图以及这些学生对自己所持手机的满意度统计表如下:

(Ⅰ)随机选取1名该校学生,估计该生持有 品牌手机的概率;
品牌手机的概率;
(Ⅱ)随机选取1名该校学生,估计该生持有 或
或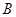 品牌手机且感到满意的概率;
品牌手机且感到满意的概率;
(Ⅲ) 两种品牌的手机哪种市场前景更好?(直接写出结果,不必证明)
两种品牌的手机哪种市场前景更好?(直接写出结果,不必证明)