(本题4分)如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:
(1)将△ABC沿x轴翻折后再沿x轴向右平移1个单位,图中画出平移后的△ 。若△ABC内有一点P(a,b),则经过两次变换后点P的坐标变为_____________
。若△ABC内有一点P(a,b),则经过两次变换后点P的坐标变为_____________
(2)作出△ABC关于坐标原点O成中心对称的△ .
.
(3)若将△ABC绕某点逆时针旋转90°后,其对应点分别为 (2,1),
(2,1), (4,0),
(4,0), (3,-2),则旋转中心坐标为______.
(3,-2),则旋转中心坐标为______.
相关知识点
推荐套卷
 ,其中
,其中




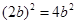 ;
;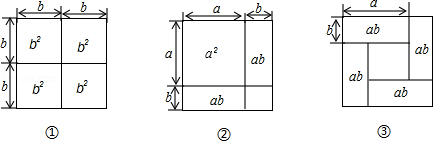
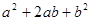 =.
=.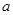 ,宽为
,宽为 的长方形纸片围成的正方形,
的长方形纸片围成的正方形, 粤公网安备 44130202000953号
粤公网安备 44130202000953号