阅读材料:为解方程(x2-1)2-5(x2-1)+4=0,我们可以将x2-1看作一个整体,然后设x2-1=y……①,那么原方程可化为y2-5y+4=0,解得y1=1,y2=4.当y=1时,x2-1=1,∴x2=2,∴x=± ;当y=4时,x2-1=4,∴x2=5,∴x=±
;当y=4时,x2-1=4,∴x2=5,∴x=± ,故原方程的解为x1=
,故原方程的解为x1= ,x2=
,x2= ,x3=
,x3= ,x4=
,x4= .
.
解答问题:(1)上述解题过程,在由原方程得到方程①的过程中,利用_________法达到了解方程的目的,体现了转化的数学思想;
(2)请利用以上知识解方程x4-x2-6=0.
相关知识点
推荐套卷
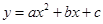 取得最小值-1,并且与y轴交于点C(0,3),与x轴交于点A、B(A在B的右边)。
取得最小值-1,并且与y轴交于点C(0,3),与x轴交于点A、B(A在B的右边)。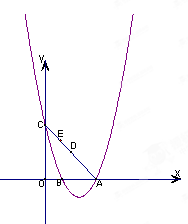
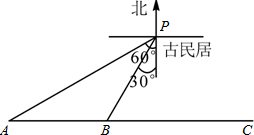
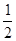 x2+bx-2与x轴交于A、B两点,与y 轴交于C点,且A(一1,0).
x2+bx-2与x轴交于A、B两点,与y 轴交于C点,且A(一1,0).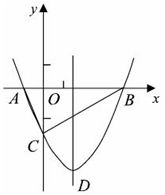
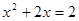 ;(2)求值:
;(2)求值: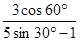
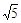 ,PB=
,PB=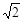 ,PC=1,求∠BPC的度数.
,PC=1,求∠BPC的度数.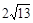 ,PB=4,PC=2.
,PB=4,PC=2.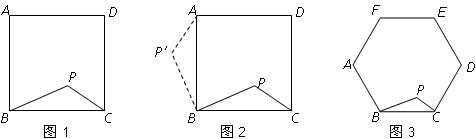
 粤公网安备 44130202000953号
粤公网安备 44130202000953号