（本小题满分14分）现有一个以OA、OB为半径的扇形池塘，在OA、OB上分别取点C、D，作DE∥OA、CF∥OB交弧AB于点E、F，且BD = AC，现用渔网沿着DE、EO、OF、FC将池塘分成如图所示的三种的养殖区域．若OA=1km，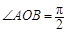
，
．
（1）求区域Ⅱ的总面积；
（2）若养殖区域Ⅰ、Ⅱ、Ⅲ的每平方千米的年收入分别是15万元、20万元、10万元，记年总收入为y万元． 试问当
为多少时，年总收入最大？
相关试题
中，角
所对的边分别为
。
，且
，求
的值。
,求
且满足
。
的值；
，判别
的符号且说明理由；
时，关于
的方程
有实数解，求实数
的取值范围。
，其中
。
；
时，判别
时
的最小值；
时恒有 
，求
的取值范围。
；（2）若
,求实数
的取值范围。
。
的图象，（2）证明：函数
在
上是增函数
推荐套卷
（本小题满分14分）现有一个以OA、OB为半径的扇形池塘，在OA、OB上分别取点C、D，作DE∥OA、CF∥OB交弧AB于点E、F，且BD = AC，现用渔网沿着DE、EO、OF、FC将池塘分成如图所示的三种的养殖区域．若OA=1km，，．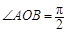
（1）求区域Ⅱ的总面积；
（2）若养殖区域Ⅰ、Ⅱ、Ⅲ的每平方千米的年收入分别是15万元、20万元、10万元，记年总收入为y万元． 试问当为多少时，年总收入最大？
粤公网安备 44130202000953号