（本小题满分14分）如图，已知三棱锥A—BPC中，AP⊥PC， AC⊥BC，M为AB中点，D为PB中点， 且△PMB为正三角形．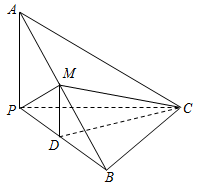
（1）求证：DM∥平面APC；
（2）求证：平面ABC⊥平面APC；
（3）若BC=4，AB=20，求三棱锥D—BCM的体积．
相关试题
，F为CE上的点，且BF
平面ACE，AC与BD交于点G
在
上的最大值和最小值.
作曲线
的切线，求此切线的方程.
中，直线L的方程为x-y+4=0，曲线C的参数方程
截圆心在点
的圆
所得弦长为
.
的圆相关知识点
推荐套卷
（本小题满分14分）如图，已知三棱锥A—BPC中，AP⊥PC， AC⊥BC，M为AB中点，D为PB中点， 且△PMB为正三角形．
（1）求证：DM∥平面APC；
（2）求证：平面ABC⊥平面APC；
（3）若BC=4，AB=20，求三棱锥D—BCM的体积．
粤公网安备 44130202000953号