(1)(本小题6分)在平面直角坐标系中,已知某点 ,直线
,直线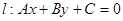 .求证:点P到直线
.求证:点P到直线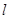 的距离
的距离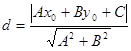
(2)(本小题7分)已知抛物线C: 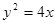 的焦点为F,点P(2,0),O为坐标原点,过P的直线
的焦点为F,点P(2,0),O为坐标原点,过P的直线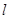 与抛物线C相交于A,B两点,若向量
与抛物线C相交于A,B两点,若向量 在向量
在向量 上的投影为n,且
上的投影为n,且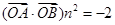 ,求直线
,求直线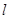 的方程.
的方程.
相关知识点
推荐套卷
(1)(本小题6分)在平面直角坐标系中,已知某点 ,直线
,直线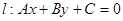 .求证:点P到直线
.求证:点P到直线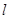 的距离
的距离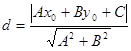
(2)(本小题7分)已知抛物线C: 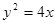 的焦点为F,点P(2,0),O为坐标原点,过P的直线
的焦点为F,点P(2,0),O为坐标原点,过P的直线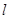 与抛物线C相交于A,B两点,若向量
与抛物线C相交于A,B两点,若向量 在向量
在向量 上的投影为n,且
上的投影为n,且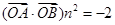 ,求直线
,求直线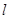 的方程.
的方程.