如图1，已知点D在AC上，△ABC和△ADE都是等腰直角三角

更新 2022-09-03
科目数学
题型解答题
难度中等
浏览 1833

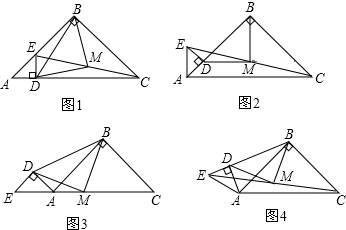
如图1，已知点D在AC上，△ABC和△ADE都是等腰直角三角形，点M为EC的中点．
（1）求证：△BMD为等腰直角三角形．
（2）将△ADE绕点A逆时针旋转45°，如图2中的“△BMD为等腰直角三角形”是否仍然成立？请说明理由．
（3）将△ADE绕点A逆时针旋转135°，如图3中的“△BMD为等腰直角三角形”成立吗？（不用说明理由）．
（4）我们是否可以猜想，将△ADE绕点A任意旋转一定的角度，如图4中的“△BMD为等腰直角三角形”均成立？（不用说明理由）．

登录免费查看答案和解析

相关试题

为了解某校某年级学生一分钟跳绳情况，对该年级全部360名学生进行一分钟跳绳次数的测试，并把测得数据分成四组，绘制成如图所示的频数表和未完成的频数分布直方图（每一组不含前一个边界值，含后一个边界值）．

某校某年级360名学生一分钟跳绳次数的频数表

组别（次 $)$	频数
$100 ~ 130$	48
$130 ~ 160$	96
$160 ~ 190$	$a$
$190 ~ 220$	72

（1）求 $a$ 的值；

（2）把频数分布直方图补充完整；

（3）求该年级一分钟跳绳次数在190次以上的学生数占该年级全部学生数的百分比．

题型：未知
难度：未知

收藏答案/解析

以下是圆圆解不等式组 $\{\begin{matrix} 2 (1 + x) > - 1 ① \\ - (1 - x) > - 2 ② \end{matrix}$ 的解答过程：

解：由①，得 $2 + x > - 1$ ，

所以 $x > - 3$ ．

由②，得 $1 - x > 2$ ，

所以 $- x > 1$ ，

所以 $x > - 1$ ．

所以原不等式组的解是 $x > - 1$ ．

圆圆的解答过程是否有错误？如果有错误，请写出正确的解答过程．

题型：未知
难度：未知

收藏答案/解析

已知抛物线 $y = - 2 x^{2} + bx + c$ 经过点 $(0, - 2)$ ，当 $x < - 4$ 时， $y$ 随 $x$ 的增大而增大，当 $x > - 4$ 时， $y$ 随 $x$ 的增大而减小．设 $r$ 是抛物线 $y = - 2 x^{2} + bx + c$ 与 $x$ 轴的交点（交点也称公共点）的横坐标， $m = \frac{r^{9} + r^{7} - 2 r^{5} + r^{3} + r - 1}{r^{9} + 60 r^{5} - 1}$ ．

（1）求 $b$ 、 $c$ 的值；

（2）求证： $r^{4} - 2 r^{2} + 1 = 60 r^{2}$ ；

（3）以下结论： $m < 1$ ， $m = 1$ ， $m > 1$ ，你认为哪个正确？请证明你认为正确的那个结论．

题型：未知
难度：未知

收藏答案/解析

如图， $AB$ 是 $⊙ O$ 的直径，点 $C$ 是 $⊙ O$ 上异于 $A$ 、 $B$ 的点，连接 $AC$ 、 $BC$ ，点 $D$ 在 $BA$ 的延长线上，且 $∠ DCA = ∠ ABC$ ，点 $E$ 在 $DC$ 的延长线上，且 $BE ⊥ DC$ ．

（1）求证： $DC$ 是 $⊙ O$ 的切线；

（2）若 $\frac{OA}{OD} = \frac{2}{3}$ ， $BE = 3$ ，求 $DA$ 的长．

题型：未知
难度：未知

收藏答案/解析

某鲜花销售公司每月付给销售人员的工资有两种方案．

方案一：没有底薪，只付销售提成；

方案二：底薪加销售提成．

如图中的射线 $l_{1}$ ，射线 $l_{2}$ 分别表示该鲜花销售公司每月按方案一，方案二付给销售人员的工资 $y_{1}$ （单位：元）和 $y_{2}$ （单位：元）与其当月鲜花销售量 $x$ （单位：千克） $(x ⩾ 0)$ 的函数关系．

（1）分别求 $y_{1}$ 、 $y_{2}$ 与 $x$ 的函数解析式（解析式也称表达式）；

（2）若该公司某销售人员今年3月份的鲜花销售量没有超过70千克，但其3月份的工资超过2000元．这个公司采用了哪种方案给这名销售人员付3月份的工资？

题型：未知
难度：未知

收藏答案/解析

推荐套卷

热门套卷