如图，直线CP是AB的中垂线且交AB于P，其中AP=2CP．甲、乙两人想在AB上取两点D、E，使得AD=DC=CE=EB，其作法如下：
（甲）作∠ACP、∠BCP之角平分线，分别交AB于D、E，则D、E即为所求；
（乙）作AC、BC之中垂线，分别交AB于D、E，则D、E即为所求．
对于甲、乙两人的作法，下列判断何者正确（ ）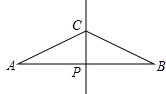
A． 两人都正确
B． 两人都错误
C． 甲正确，乙错误
D． 甲错误，乙正确
相关试题
如图，直线CP是AB的中垂线且交AB于P，其中AP=2CP．甲、乙两人想在AB上取两点D、E，使得AD=DC=CE=EB，其作法如下：
（甲）作∠ACP、∠BCP之角平分线，分别交AB于D、E，则D、E即为所求；
（乙）作AC、BC之中垂线，分别交AB于D、E，则D、E即为所求．
对于甲、乙两人的作法，下列判断何者正确（ ）
A． 两人都正确
B． 两人都错误
C． 甲正确，乙错误
D． 甲错误，乙正确
米，那么它的一百万倍相当于（ ）
粤公网安备 44130202000953号