如图,有A、B两个转盘,其中转盘A被分成4等份,转盘B被分成3等份,并在每一份内标上数字。现甲、乙两人同时各转动其中一个转盘,转盘停止后(当指针指在边界线上时视为无效,重转),若将A转盘指针指向的数字记为x,B转盘指针指向的数字记为y,从而确定点P的坐标为P(x,y)。记S=x+y。
(1)请用列表或画树状图的方法写出所有可能得到的点P的坐标;
(2)李刚为甲、乙两人设计了一个游戏:当S<6时甲获胜,否则乙获胜。你认为这个游戏公平吗?对谁有利?
相关知识点
推荐套卷
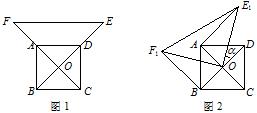
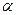 角得到△E1OF1(如图2).
角得到△E1OF1(如图2).
 粤公网安备 44130202000953号
粤公网安备 44130202000953号