（本小题满分12分）某鱼类养殖户在一个鱼池中养殖一种鱼，每季养殖成本为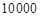
元，此鱼的市场价格和鱼池的产量均具有随机性，且互不影响，其具体情况如下表：
鱼池产量 |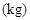
 |
 |
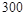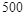| 概 率 |
 |
|
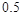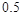| 鱼的市场价格（元/ |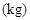
 |
 |
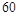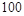| 概 率 |
 |
 |
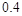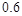（Ⅰ）设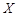
表示在这个鱼池养殖
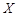季这种鱼的利润，求的分布列和期望；
（Ⅱ）若在这个鱼池中连续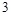
季养殖这种鱼，求这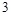季中至少有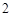
季的利润不少于
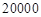元的概率．
，且与圆
相切于点
的圆
的方程，并判断两圆是外切还是内切？
经过点
，且与圆
相交与
两点，截得的弦长为
，求
：
象限
的取值范围
直线
：
若直线
的取值范围？
，并且经过原点和点
的圆的方程推荐套卷
（本小题满分12分）某鱼类养殖户在一个鱼池中养殖一种鱼，每季养殖成本为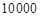元，此鱼的市场价格和鱼池的产量均具有随机性，且互不影响，其具体情况如下表：
| 鱼池产量 |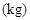
|
|
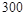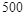| 概 率 |
|
|
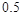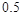| 鱼的市场价格（元/ |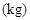
|
|
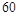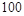| 概 率 |
|
|
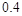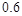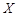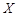（Ⅰ）设表示在这个鱼池养殖季这种鱼的利润，求的分布列和期望；
（Ⅱ）若在这个鱼池中连续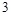季养殖这种鱼，求这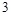季中至少有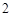季的利润不少于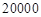元的概率．
粤公网安备 44130202000953号