如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.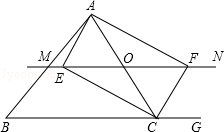
(1)判断OE与OF的大小关系?并说明理由;
(2)当点O运动到何处时,四边形AECF是矩形?并说出你的理由;
(3)在(2)的条件下,当△ABC满足什么条件时,四边形AECF会是正方形.
不要写理由.
推荐套卷
如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)判断OE与OF的大小关系?并说明理由;
(2)当点O运动到何处时,四边形AECF是矩形?并说出你的理由;
(3)在(2)的条件下,当△ABC满足什么条件时,四边形AECF会是正方形.
不要写理由.