(本小题满分15分)为合理用电缓解电力紧张,某市将试行“峰谷电价”计费方法,在高峰用电时段,即居民户每日8时至22时,电价每千瓦时为0.56元,其余时段电价每千瓦时为0.28元.而目前没有实行“峰谷电价”的居民用户电价为每千瓦时为0.53元.若总用电量为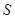 千瓦时,设高峰时段用电量为
千瓦时,设高峰时段用电量为 千瓦时.
千瓦时.
(1)写出实行峰谷电价的电费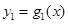 及现行电价的电费的
及现行电价的电费的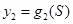 函数解析式及电费总差额
函数解析式及电费总差额 的解析式;
的解析式;
(2)对于用电量按时均等的电器(在全天任何相同长的时间内,用电量相同),采用峰谷电价的计费方法后是否能省钱?说明你的理由.
推荐套卷
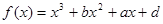 的图象过点P(0,2),且在点M
的图象过点P(0,2),且在点M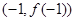 处的切线方程为
处的切线方程为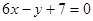 .
.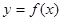 的解析式;
的解析式;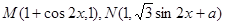
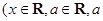 是常数),且
是常数),且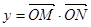 (其中
(其中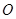 为坐标原点).
为坐标原点).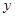 关于
关于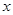 的函数关系式
的函数关系式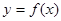 ;
;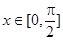 时,
时,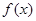 的最大值为4,求
的最大值为4,求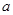 的值.
的值.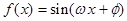 (
(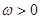 ,
,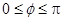 )为偶函数,其图象上相邻的两个最高点之间的距离为
)为偶函数,其图象上相邻的两个最高点之间的距离为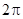 .
.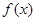 的解析式;
的解析式;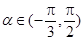 ,
,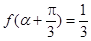 ,求
,求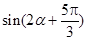 的值.
的值.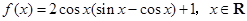 .
.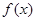 的单调递增取区间;
的单调递增取区间;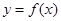 的图象向左平移
的图象向左平移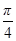 个单位后,再将图象上各点的横坐标伸长到原来的2倍,纵坐标不变,得到函数
个单位后,再将图象上各点的横坐标伸长到原来的2倍,纵坐标不变,得到函数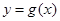 的图象,求
的图象,求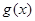 的最大值及取得最大值时的
的最大值及取得最大值时的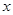 的集合.
的集合.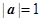 ,
,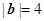 ,且向量
,且向量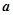 与
与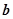 不共线.
不共线.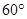 ,求
,求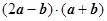 ;
;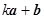 与
与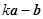 互相垂直,求
互相垂直,求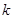 的值.
的值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号