如图，在平面直角坐标系中，△ABC三个顶点的坐标分别为A（0，4），B（﹣3，5），C（﹣4，1）．
（1）把△ABC向右平移2个单位得△A1B1C1，请画出△A1B1C1，并写出点A1的坐标；
（2）把△ABC绕原点O旋转180°得到△A2B2C2，请画出△A2B2C2．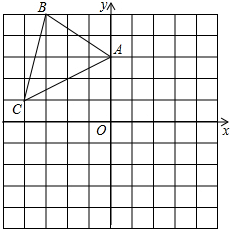
相关试题
如图，在平面直角坐标系中，△ABC三个顶点的坐标分别为A（0，4），B（﹣3，5），C（﹣4，1）．
（1）把△ABC向右平移2个单位得△A1B1C1，请画出△A1B1C1，并写出点A1的坐标；
（2）把△ABC绕原点O旋转180°得到△A2B2C2，请画出△A2B2C2．
；
，那么
（填入 “=”或 “≠ ”）
，请求出
的值。
的方程：
与
有相同的解，求关于
的方程
的解．
，计算
．某同学做此题时误将
看成了
，求得
=
，若
，请你帮助他求得正确答案．
，其中
．有位同学把
错抄成
，但他的计算结果也是正确的，试通过计算说明其中的道理．-
粤公网安备 44130202000953号