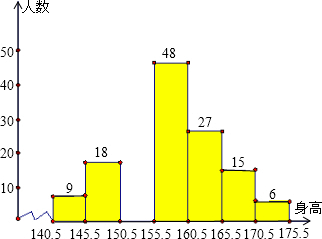
要了解某地区九年级学生的身高情况，从中随机抽取150名学生的身高作为一个样本，身高均在141cm～175cm之间（取整数厘米），整理后分成7组，绘制出频数分布直方图（不完整）．根据图中提供的信息，解答下列问题：
（1）补全频数分布直方图；
（2）该地区共有3000名九年级学生，估计其中身高不低于161cm的人数；
（3）估计该地区九年级学生身高不低于151cm的概率．