如图，椭圆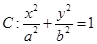
（
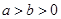）的离心率
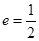，短轴的两个端点分别为B1、B2，焦点为F1、F2，四边形F1 B1F2 B2的内切圆半径为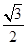
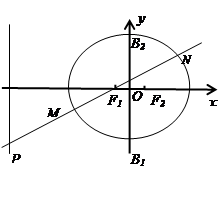
（1）求椭圆C的方程；
（2）过左焦点F1的直线交椭圆于M、N两点，交直线
于点P，设
，
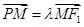，试证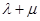
为定值，并求出此定值．
相关试题
中，角
的对边分别为
，向量
，
，且
；
的值；
，
，求角
的大小及向量
在
方向上的投影值.
是公差不为零的等差数列，
，且
是
和
的等比中项，求：
.
，
，（1）若
与
垂直，求
的值；（2）若
，求
中，
其前
项和
满足：
的前
项和
满足:
,求数列
的前
.推荐套卷
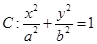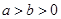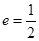如图，椭圆 （）的离心率，短轴的两个端点分别为B1、B2，焦点为F1、F2，四边形F1 B1F2 B2的内切圆半径为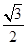
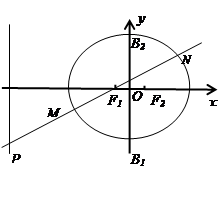
（1）求椭圆C的方程；
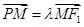（2）过左焦点F1的直线交椭圆于M、N两点，交直线于点P，设，，试证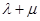为定值，并求出此定值．
粤公网安备 44130202000953号