对于数列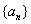 ,规定数列
,规定数列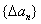 为数列
为数列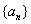 的一阶差分数列,其中
的一阶差分数列,其中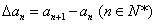 ;一般地,规定
;一般地,规定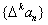 为
为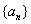 的k阶差分数列,其中
的k阶差分数列,其中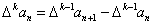 且k∈N*,k≥2。
且k∈N*,k≥2。
(1)已知数列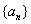 的通项公式
的通项公式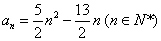 。试证明
。试证明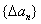 是等差数列;
是等差数列;
(2)若数列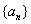 的首项a1=―13,且满足
的首项a1=―13,且满足 ,求数列
,求数列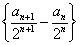 及
及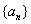 的通项公式;
的通项公式;
(3)在(2)的条件下,判断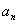 是否存在最小值;若存在,求出其最小值,若不存在,说明理由。
是否存在最小值;若存在,求出其最小值,若不存在,说明理由。
推荐套卷
对于数列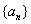 ,规定数列
,规定数列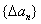 为数列
为数列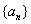 的一阶差分数列,其中
的一阶差分数列,其中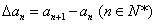 ;一般地,规定
;一般地,规定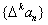 为
为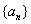 的k阶差分数列,其中
的k阶差分数列,其中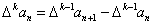 且k∈N*,k≥2。
且k∈N*,k≥2。
(1)已知数列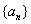 的通项公式
的通项公式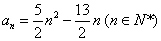 。试证明
。试证明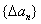 是等差数列;
是等差数列;
(2)若数列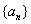 的首项a1=―13,且满足
的首项a1=―13,且满足 ,求数列
,求数列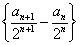 及
及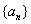 的通项公式;
的通项公式;
(3)在(2)的条件下,判断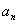 是否存在最小值;若存在,求出其最小值,若不存在,说明理由。
是否存在最小值;若存在,求出其最小值,若不存在,说明理由。