(理科)在平面直角坐标系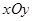 中,椭圆
中,椭圆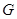 的中心为坐标原点,左焦点为
的中心为坐标原点,左焦点为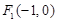 ,
, 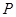 为椭圆
为椭圆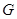 的上顶点,且
的上顶点,且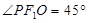 .
.
(Ⅰ)求椭圆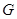 的标准方程;
的标准方程;
(Ⅱ)已知直线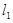 :
: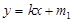 与椭圆
与椭圆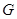 交于
交于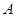 ,
,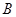 两点,直线
两点,直线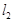 :
: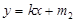 (
(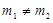 )与椭圆
)与椭圆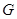 交于
交于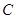 ,
,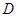 两点,且
两点,且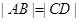 ,如图所示.
,如图所示.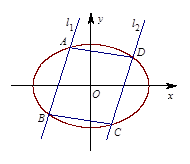
(ⅰ)证明: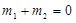 ;
;
(ⅱ)求四边形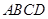 的面积
的面积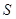 的最大值.
的最大值.
推荐套卷
(理科)在平面直角坐标系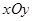 中,椭圆
中,椭圆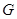 的中心为坐标原点,左焦点为
的中心为坐标原点,左焦点为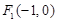 ,
, 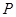 为椭圆
为椭圆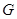 的上顶点,且
的上顶点,且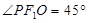 .
.
(Ⅰ)求椭圆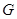 的标准方程;
的标准方程;
(Ⅱ)已知直线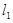 :
: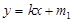 与椭圆
与椭圆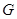 交于
交于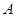 ,
,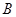 两点,直线
两点,直线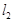 :
: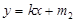 (
(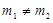 )与椭圆
)与椭圆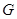 交于
交于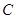 ,
,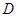 两点,且
两点,且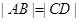 ,如图所示.
,如图所示.
(ⅰ)证明: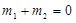 ;
;
(ⅱ)求四边形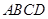 的面积
的面积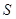 的最大值.
的最大值.