(本小题满分12分)如图,四边形ABCD为梯形,AB∥CD, 平面ABCD,
平面ABCD, ,
,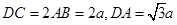 ,E为BC中点.
,E为BC中点.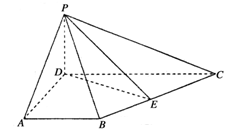
(1)求证:平面 平面PDE;
平面PDE;
(2)线段PC上是否存在一点F,使PA//平面BDF?若有,请找出具体位置,并进行证明;若无,请分析说明理由.
推荐套卷
(本小题满分12分)如图,四边形ABCD为梯形,AB∥CD, 平面ABCD,
平面ABCD, ,
,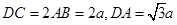 ,E为BC中点.
,E为BC中点.
(1)求证:平面 平面PDE;
平面PDE;
(2)线段PC上是否存在一点F,使PA//平面BDF?若有,请找出具体位置,并进行证明;若无,请分析说明理由.