(本小题满分14分)已知椭圆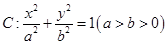 ,其中
,其中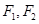 为左、右焦点,O为坐标原点.直线l与椭圆交于
为左、右焦点,O为坐标原点.直线l与椭圆交于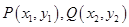 两个不同点.当直线l过椭圆C右焦点F2且倾斜角为
两个不同点.当直线l过椭圆C右焦点F2且倾斜角为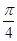 时,原点O到直线l的距离为
时,原点O到直线l的距离为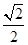 .又椭圆上的点到焦点F2的最近距离为
.又椭圆上的点到焦点F2的最近距离为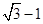 .
.
(1)求椭圆C的方程;
(2)以OP,OQ为邻边做平行四边形OQNP,当平行四边形OQNP面积为 时,求平行四边形OQNP的对角线之积
时,求平行四边形OQNP的对角线之积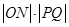 的最大值;
的最大值;
(3)若抛物线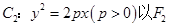 为焦点,在抛物线C2上任取一点S(S不是原点O),以OS为直径作圆,交抛物线C2于另一点R,求该圆面积最小时点S的坐标.
为焦点,在抛物线C2上任取一点S(S不是原点O),以OS为直径作圆,交抛物线C2于另一点R,求该圆面积最小时点S的坐标.
相关知识点
推荐套卷
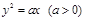 ,直线l与抛物线交于A、B,且
,直线l与抛物线交于A、B,且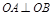 ,点
,点 在AB上,又
在AB上,又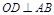 .
.
 ,点M(2,1).
,点M(2,1). ;命题q:
;命题q: .若p是真命题,且q是假命题,求实数x的取值范围.
.若p是真命题,且q是假命题,求实数x的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号