张华在一次数学活动中，利用“在面积一定的矩形中，正方形的周长最短”的结论，推导出“式子x+
（x＞0）的最小值是2”．其推导方法如下：在面积是1的矩形中设矩形的一边长为x，则另一边长是，矩形的周长是2（x+）；当矩形成为正方形时，就有x=（0＞0），解得x=1，这时矩形的周长2（x+）=4最小，因此x+（x＞0）的最小值是2．模仿张华的推导，你求得式子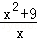
（x＞0）的最小值是（ ）
| A．2 | B．1 | C．6 | D．10 |
相关试题
张华在一次数学活动中，利用“在面积一定的矩形中，正方形的周长最短”的结论，推导出“式子x+（x＞0）的最小值是2”．其推导方法如下：在面积是1的矩形中设矩形的一边长为x，则另一边长是，矩形的周长是2（x+）；当矩形成为正方形时，就有x=（0＞0），解得x=1，这时矩形的周长2（x+）=4最小，因此x+（x＞0）的最小值是2．模仿张华的推导，你求得式子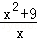（x＞0）的最小值是（ ）
| A．2 | B．1 | C．6 | D．10 |
的解集是（）
粤公网安备 44130202000953号