某市为了了解“陕西分类招生考试”宣传情况，从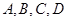
四所中学的学生当中随机抽取50名学生参加问卷调查，已知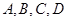四所中学各抽取的学生人数分别为15,20,10,5.
（Ⅰ）从参加问卷调查的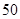
名学生中随机抽取两名学生,求这两名学生来自同一所中学的概率；
（Ⅱ）在参加问卷调查的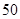名学生中,从来自
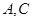两所中学的学生当中随机抽取两名学生,用
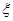表示抽得
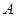中学的学生人数,求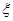的分布列及期望值.
相关试题
。过A、B、C 做平行四边形ABCD。 求点D的坐标及此平行四边形的对角线BD的长。
，
，求
， 
，使
在
上的最小值为
，若存在，求出推荐套卷
某市为了了解“陕西分类招生考试”宣传情况，从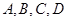四所中学的学生当中随机抽取50名学生参加问卷调查，已知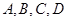四所中学各抽取的学生人数分别为15,20,10,5.
（Ⅰ）从参加问卷调查的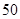名学生中随机抽取两名学生,求这两名学生来自同一所中学的概率；
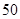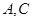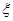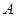（Ⅱ）在参加问卷调查的名学生中,从来自两所中学的学生当中随机抽取两名学生,用表示抽得中学的学生人数,求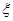的分布列及期望值.
粤公网安备 44130202000953号