（本小题满分12分）袋子中装有大小相同的白球和红球共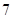
个，从袋子中任取
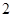个球都是白球的概率为
，每个球被取到的机会均等．现从袋子中每次取
个球，如果取出的是白球则不再放回，设在取得红球之前已取出的白球个数为
．
（1）求袋子中白球的个数；
（2）求的分布列和数学期望．
：
；
：
，若命题
的取值范围..
前
项之和为
，
，
，求
和
中，
所对的边长分别为
，设
和
， 
的值．
恒成立，求实数m的取值范围.
，
．
，求
的值．
，求
的单调的递减区间；推荐套卷
（本小题满分12分）袋子中装有大小相同的白球和红球共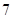个，从袋子中任取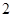个球都是白球的概率为，每个球被取到的机会均等．现从袋子中每次取个球，如果取出的是白球则不再放回，设在取得红球之前已取出的白球个数为．
（1）求袋子中白球的个数；
（2）求的分布列和数学期望．
粤公网安备 44130202000953号