（本小题满分12分）点P为抛物线y=x2-2mx+m2（m为常数，m>0）上任一点，将抛物线绕顶点G逆时针旋转90°后得到的新图象与y轴交于A，B两点（点A在点B的上方），点Q为点P旋转后的对应点．
（1）当m=2，点P横坐标为4时，求Q点的坐标；
（2）设点Q（a，b），用含m，b的代数式表示a；（直接写出结果）
（3）如图，点Q在第一象限内，点D在并轴的正半轴上，点C为OD的中点，QD平分∠AQC，AQ=2QC，当QD=m时，求m的值．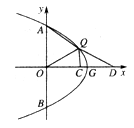
相关试题
随着人们节能意识的增强，节能产品进入千家万户，今年1月小明家将天燃气热水器换成了太阳能热水器．去年12月份小明家的燃气费是96元，从今年1月份起天燃气价格每立方米上涨25%，小明家2月份的用气量比去年12月份少10立方米，2月份的燃气费是90元．问小明家2月份用气多少立方米．
，其中
.
的整数解．
．相关知识点
推荐套卷
粤公网安备 44130202000953号