如图，在平面直角坐标系中，已知OA=12厘米，OB=6厘米．点P从点O开始沿OA边向点A以1厘米/秒的速度移动；点Q从点B开始沿BO边向点O以1厘米/秒的速度移动．如果P、Q同时出发，用t（秒）表示移动的时间（0≤t≤6），那么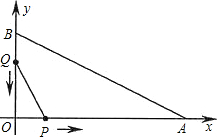
（1）设△POQ的面积为y，求y关于t的函数解析式；
（2）当△POQ的面积最大时，将△POQ沿直线PQ翻折后得到△PCQ，试判断点C是否落在直线AB上，并说明理由；
（3）当t为何值时，△POQ与△AOB相似．
相关试题
和
有公共解，求a,b的值.
的解是
求方程组
的解”提出了各自的想法．甲说：“这个题目好像条件不够，不能求解．”乙说：“它们的系数有一定的规律，可以试试．”丙说：“能不能把第二个方程组中两个方程的两边都除以5，通过换元的方法来解决．”参考他们的讨论，你认为这个题目的解是．相关知识点
推荐套卷
粤公网安备 44130202000953号