（本小题满分12分）如图，摩天轮上一点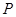
在
时刻距离地面高度满足
，已知某摩天轮的半径为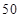
米，点
距地面的高度为
米，摩天轮做匀速转动，每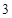
分钟转一圈，点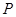的起始位置在摩天轮的最低点处．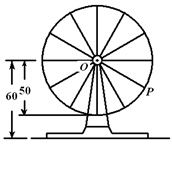
（1）根据条件写出
（米）关于（分钟）的解析式；
（2）在摩天轮转动的一圈内，有多长时间点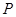距离地面超过
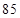米?
相关试题
+(a2-5a-6)i(a∈R),试求实数a分别取什么值时，z分别为：
.
(
+
+
).
＜2与
＜2中至少有一个成立.
; (2)
;
+
; (4) 
.相关知识点
推荐套卷
（本小题满分12分）如图，摩天轮上一点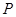在时刻距离地面高度满足，已知某摩天轮的半径为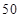米，点距地面的高度为米，摩天轮做匀速转动，每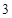分钟转一圈，点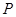的起始位置在摩天轮的最低点处．
（1）根据条件写出（米）关于（分钟）的解析式；
（2）在摩天轮转动的一圈内，有多长时间点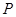距离地面超过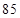米?
粤公网安备 44130202000953号