(年浙江台州12分)某公司经营杨梅业务,以3万元/吨的价格向农户收购杨梅后,分拣成A、B两类,A类杨梅包装后直接销售,B类杨梅深加工再销售.A类杨梅的包装成本为1万元/吨,根据市场调查,它的平均销售价格y(单位∶万元/吨)与销售数量x(x≥2)(单位∶吨)之间的函数关系式如图,B类杨梅深加工总费用s(单位:万元)与加工数量t(单位∶吨)之间的函数关系是s=12+3t,平均销售价格为9万元/吨.
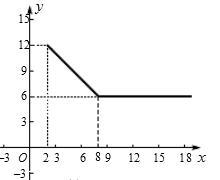
(1)直接写出A类杨梅平均销售价格y与销售量x这间的函数关系式;
(2)第一次,该公司收购了20吨杨梅,其中A类杨梅x吨,经营这批杨梅所获得的毛利润为w万元(毛利润=销售总收人-经营总成本).
①求w关于x的函数关系式;
②若该公司获得了30万元毛利润,问∶用于直销的A类杨梅有多少吨?
(3)第二次该公司准备投人132万元资金,请设计-种经营方案,使公司获得最大毛利润,并求出最大毛利润.