如图1所示的晾衣架，支架主视图的基本图形是菱形，其示意图如图2，晾衣架伸缩时，点G在射线DP上滑动，∠CED的大小也随之发生变化，已知每个菱形边长均等于20cm，且AH=DE=EG=20cm．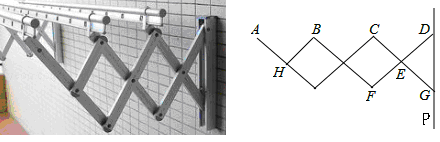
（1）当∠CED=60°时，求C、D两点间的距离；
（2）当∠CED由60°变为120°时，点A向左移动了多少cm？（结果精确到0.1cm）
（3）设DG=xcm，当∠CED的变化范围为60°～120°（包括端点值）时，求x的取值范围．（结果精确到0.1cm）（参考数据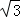
≈1.732）
相关试题
在 中， ， ，将 绕点 顺时针旋转一定的角度 得到 ，点 、 的对应点分别是 、 ．
（1）当点 恰好在 上时，如图1，求 的大小；
（2）若 时，点 是边 中点，如图2，求证：四边形 是平行四边形．
相关知识点
推荐套卷
粤公网安备 44130202000953号