(本小题满分13分)在平面直角坐标系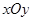 中,椭圆
中,椭圆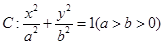 过点
过点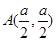 和点
和点 .
.
(1)求椭圆 的方程;
的方程;
(2)已知点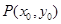 在椭圆
在椭圆 上,
上,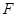 为椭圆的左焦点,直线
为椭圆的左焦点,直线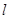 的方程为
的方程为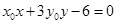 .
.
(i)求证:直线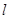 与椭圆
与椭圆 有唯一的公共点;
有唯一的公共点;
(ii)若点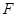 关于直线
关于直线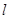 的对称点为
的对称点为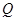 ,探索:当点
,探索:当点 在椭圆
在椭圆 上运动时,直线
上运动时,直线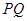 是否过定点?若过定点,求出此定点的坐标;若不过定点,请说明理由.
是否过定点?若过定点,求出此定点的坐标;若不过定点,请说明理由.
推荐套卷
(本小题满分13分)在平面直角坐标系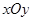 中,椭圆
中,椭圆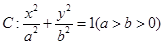 过点
过点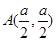 和点
和点 .
.
(1)求椭圆 的方程;
的方程;
(2)已知点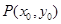 在椭圆
在椭圆 上,
上,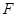 为椭圆的左焦点,直线
为椭圆的左焦点,直线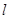 的方程为
的方程为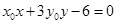 .
.
(i)求证:直线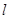 与椭圆
与椭圆 有唯一的公共点;
有唯一的公共点;
(ii)若点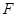 关于直线
关于直线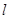 的对称点为
的对称点为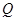 ,探索:当点
,探索:当点 在椭圆
在椭圆 上运动时,直线
上运动时,直线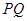 是否过定点?若过定点,求出此定点的坐标;若不过定点,请说明理由.
是否过定点?若过定点,求出此定点的坐标;若不过定点,请说明理由.