已知抛物线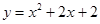

(1)、该抛物线的对称轴是 ,顶点坐标 ;
(2)、选取适当的数据填入下表,并在直角坐标系内描点画出该抛物线的图象;
| x |
… |
|
|
|
|
|
… |
| y |
… |
|
|
|
|
|
… |
(3)、若该抛物线上两点A(x1,y1),B(x2,y2)的横坐标满足x1>x2>1,试比较y1与y2的大小.
相关知识点
推荐套卷
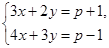 的解满足x>y,求p的取值范围.
的解满足x>y,求p的取值范围.
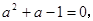
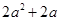 的值;
的值;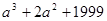 的值。
的值。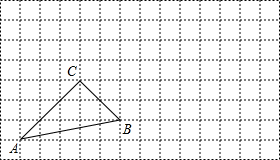
 粤公网安备 44130202000953号
粤公网安备 44130202000953号