某景区的旅游线路如图1所示,其中A为入口,B,C,D为风景点,E为三岔路的交汇点,图1中所给数据为相应两点间的路程(单位:km).甲游客以一定的速度沿线路“A→D→C→E→A”步行游览,在每个景点逗留的时间相同,当他回到A处时,共用去3h.甲步行的路程s(km)与游览时间t(h)之间的部分函数图象如图2所示.
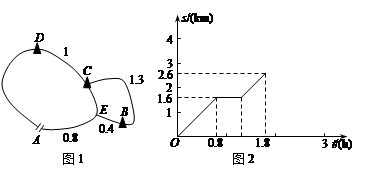
(1)求甲在每个景点逗留的时间,并补全图象;
(2)求C,E两点间的路程;
(3)乙游客与甲同时从A处出发,打算游完三个景点后回到A处,两人相约先到者在A处等候, 等候时间不超过10分钟.如果乙的步行速度为3km/h,在每个景点逗留的时间与甲相同,他们的约定能否实现?请说明理由.