甲骑自行车、乙骑摩托车沿相同路线由A地到B地，行驶过程中路程与时间的函数关系的图象如图．根据图象解决下列问题：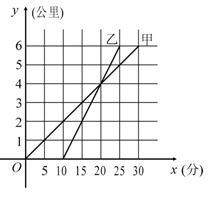
（1）谁先出发？先出发多少时间？谁先到达终点？先到多少时间？
（2）分别求出甲、乙两人的行驶速度；
（3）在什么时间段内，两人均行驶在途中（不包括起点和终点）？在这一时间段内，请你根据下列情形，分别列出关于行驶时间x的方程或不等式（不化简，也不求解）：① 甲在乙的前面；② 甲与乙相遇；③ 甲在乙后面.
相关试题
如图，抛物线 与 轴交于 ， 两点．
（1）若过点 的直线 是抛物线的对称轴．
①求抛物线的解析式；
②对称轴上是否存在一点 ，使点 关于直线 的对称点 恰好落在对称轴上．若存在，请求出点 的坐标；若不存在，请说明理由．
（2）当 ， 时，函数值 的最大值满足 ，求 的取值范围．
相关知识点
推荐套卷
粤公网安备 44130202000953号