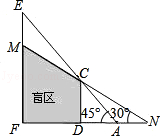
如图，CD，EF表示高度不同的两座建筑物，已知CD高15米，小明站在A处，视线越过CD，能看到它后面的建筑物的顶端E，此时小明的视角∠FAE=45°，为了能看到建筑物EF上点M的位置，小明延直线FA由点A移动到点N的位置，此时小明的视角∠FNM=30°，求AN之间的距离．