当你进入博物馆的展览厅时，你知道站在何处观赏最理想？
如图，设墙壁上的展品最高处点P距离地面a米，最低处点Q距离地面b米，观赏者的眼睛点E距离地面m米，当过P、Q、E三点的圆与过点E的水平线相切于点E时，视角∠PEQ最大，站在此处观赏最理想．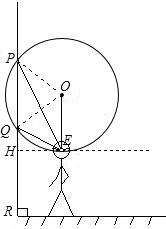
（1）设点E到墙壁的距离为x米，求a、b、m、x的关系式；
（2）当a=2.5，b=2，m=1.6，求：
（ⅰ）点E和墙壁距离x；
（ⅱ）最大视角∠PEQ的度数．（精确到1度）
相关试题
请认真观察图形，解答下列问题：
（1）根据图中条件，用两种方法表示两个阴影图形的面积的和（只需表示，不必化简）；
（2）由（1），你能得到怎样的等量关系？请用等式表示；
（3）如果图中的
（
＞
）满足
，
，求：①
的值；②
的值.
如图，在△ABC中，∠C=90°，AD所在直线是∠BAC的对称轴，DE⊥AB于E，点F在AC上，BD=DF.
求证：（1）DC=DE；
（2）CF="EB."
，其中
=-2，
=1.
粤公网安备 44130202000953号