如图,在边长为10的菱形ABCD中,对角线BD=16,点O是直线BD上的动点,OE⊥AB于E,OF⊥AD于F.
(1)对角线AC的长是 ,菱形ABCD的面积是 ;
(2)如图1,当点O在对角线BD上运动时,OE+OF的值是否发生变化?请说明理由;
(3)如图2,当点O在对角线BD的延长线上时,OE+OF的值是否发生变化?若不变,请说明理由,若变化,请探究OE、OF之间的数量关系,并说明理由.
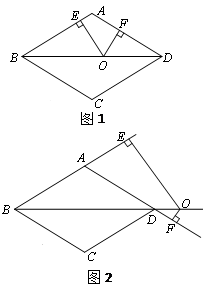
如图,在边长为10的菱形ABCD中,对角线BD=16,点O是直线BD上的动点,OE⊥AB于E,OF⊥AD于F.
(1)对角线AC的长是 ,菱形ABCD的面积是 ;
(2)如图1,当点O在对角线BD上运动时,OE+OF的值是否发生变化?请说明理由;
(3)如图2,当点O在对角线BD的延长线上时,OE+OF的值是否发生变化?若不变,请说明理由,若变化,请探究OE、OF之间的数量关系,并说明理由.
