中，AB=AC，将线段AB绕点A按逆时针方向旋转
得到线段AD,其中
.连结BD，CD， 
.
（1）若
，
,在图1中补全图形，并写出m值.
（2）如图2，当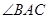
为钝角，
时 ，
值是否发生改变？证明你的猜想.
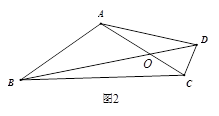
(3) 如图3，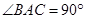
，
，BD与AC相交于点O，求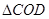
与
的面积比.
相关试题
+
﹣cd的值．
，﹣（﹣4），0，+（﹣1），1，﹣|﹣3
与﹣
．相关知识点
推荐套卷
中，AB=AC，将线段AB绕点A按逆时针方向旋转得到线段AD,其中.连结BD，CD， .
（1）若，,在图1中补全图形，并写出m值.
（2）如图2，当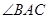为钝角，时 ，值是否发生改变？证明你的猜想.
(3) 如图3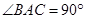， ，，BD与AC相交于点O，求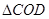与的面积比.
粤公网安备 44130202000953号