（本小题满分12分）如图，以原点O为顶点，以y轴为对称轴的抛物线E的焦点为F（0，1），点M是直线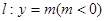
上任意一点，过点M引抛物线E的两条切线分别交x轴于点S，T，切点分别为B，A。
（Ⅰ）求抛物线E的方程；
（Ⅱ）求证：点S，T在以FM为直径的圆上；
相关试题
， 
满足条件：
， 
．
是等比数列，并求数列
项和
，并求使得
对任意
N*都成立的正整数
的最小值．
、
、
分别为
的三边
、
、
所对的角，向量
，
，且
.
，求边
}中，
，前
项和
．
项、第
项、第
项…第
项……按原来的顺序组成一个新的数列{
}，求数列{
项和
．
，
，
.
//
，求证：ΔABC为等腰三角形；
，边长
，角
，求ΔABC的面积 .
是定义在区间
上的奇函数，且
，若
时，有
.
；
对
与
恒成立，求实数
的取值范围.相关知识点
推荐套卷
（本小题满分12分）如图，以原点O为顶点，以y轴为对称轴的抛物线E的焦点为F（0，1），点M是直线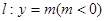上任意一点，过点M引抛物线E的两条切线分别交x轴于点S，T，切点分别为B，A。
（Ⅰ）求抛物线E的方程；
（Ⅱ）求证：点S，T在以FM为直径的圆上；
粤公网安备 44130202000953号