如图，在平面直角坐标系中，⊙M与x轴交于A、B两点，AC是⊙M的直径，过点C的直线交x轴于点D，连接BC，已知点M的坐标为（0，
），直线CD的函数解析式为y=－x＋5．
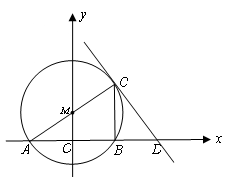
（1）点D的坐标和BC的长；
（2）求点C的坐标和⊙M的半径；
（3）求证：CD是⊙M的切线．
的一元二次方程
有实数根，
为正整数.
相关知识点
推荐套卷
如图，在平面直角坐标系中，⊙M与x轴交于A、B两点，AC是⊙M的直径，过点C的直线交x轴于点D，连接BC，已知点M的坐标为（0，），直线CD的函数解析式为y=－x＋5．
（1）点D的坐标和BC的长；
（2）求点C的坐标和⊙M的半径；
（3）求证：CD是⊙M的切线．
粤公网安备 44130202000953号