已知：如图，在△ABC中，∠C=90°，∠B=30°，AC=6，点D在边BC上，AD平分∠CAB，E为AC上的一个动点（不与A、C重合），EF⊥AB，垂足为F．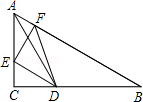
（1）求证：AD=DB；
（2）设CE=x，BF=y，求y关于x的函数解析式；
（3）当∠DEF=90°时，求BF的长？
相关试题
如图，在△ABC中，AB=AC．分别以B、C为圆心，BC长为半径在BC下方画弧，设两弧交于点D，与AB、AC的延长线分别交于点E、F，连接AD、BD、CD．
（1）求证：AD平分∠BAC；
（2）若BC=6，∠BAC＝50°，求
、
的长度之和（结果保留
）．
一个不透明的口袋中装有2个红球（记为红球1、红球2）、1个白球、1个黑球，这些球除颜色外都相同，将球摇匀．
（1）从中任意摸出1个球，恰好摸到红球的概率是；
（2）先从中任意摸出1个球，再从余下的3个球中任意摸出1个球，请用列举法（画树状图或列表）求两次都摸到红球的概率．
，其中
．
粤公网安备 44130202000953号