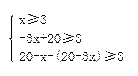某工厂有一种材料,可加工甲、乙、丙三种型号机械配件共240件,厂方计划由20个工人一天内加工完成,并要求每人只加工一种配件,根据下表提供的信息,解答下列问题:
配件种类
|
甲
|
乙
|
丙
|
每人可加工配件的数量(个)
|
16
|
12
|
10
|
每个配件获利(元)
|
6
|
8
|
5
|
(1)设加工甲种配件的人数为x,加工乙种配件的人数为y,求y与x之间的函数关系式
(2)如果加工每种配件的人数均不少于3人,那么加工配件的人数安排方案有几种?并写出每种安排方案
(3)要使此次加工配件的利润最大,应采用哪种方案?最大利润是多少?