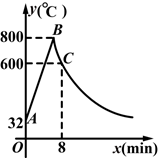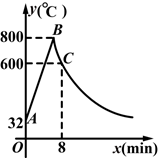
工匠制作某种金属工具要进行材料煅烧和锻造两个工序，即需要将材料煅烧到800℃，然后停止煅烧进行锻造操作．经过8min时，材料温度降为600℃．煅烧时，温度y（℃）与时间x（min）成一次函数关系；锻造时，温度y（℃）与时间x（min）成反比例函数关系（如图），已知该材料初始温度是32℃．
（1）分别求出材料煅烧和锻造时y与x的函数关系式，并且写出自变量x的取值范围；
（2）根据工艺要求，当材料温度低于480℃时，须停止操作，那么锻造的操作时间有多长？