在一个不透明的口袋里装有颜色不同的黑、白两种颜色的球共5只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
摸球的次数n
|
100
|
150
|
200
|
500
|
800
|
1000
|
摸到白球的次数m
|
58
|
96
|
116
|
295
|
484
|
601
|
摸到白球的频率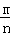
|
0.58
|
0.64
|
0.58
|
0.59
|
0.605
|
0.601
|
(1)请估计:当n很大时,摸到白球的频率将会接近 ;(精确到0.1)
(2)试估算口袋中白种颜色的球有多少只?
(3)请画树状图或列表计算:从中先摸出一球,不放回,再摸出一球;这两只球颜色不同的概率是多少?