已知某种水果的批发单价与批发量的函数关系如图所示．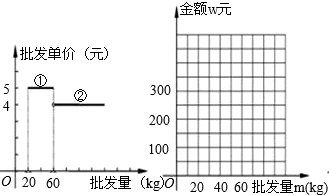
（1）请说明图中①、②两段函数图象的实际意义．
（2）写出批发该种水果的资金金额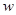
（元）与批发量
（
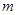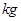）之间的函数关系式；在图中的坐标系中画出该函数图象；指出金额在什么范围内，以同样的资金可以批发到较多数量的该种水果．
，则
=______________.
，则
_______.
，则
的值为_______.
，定义一种运算“
”如下：
.那么
_______.
、
均被直线
、
所截，且
相关知识点
推荐套卷
已知某种水果的批发单价与批发量的函数关系如图所示．
（1）请说明图中①、②两段函数图象的实际意义．
（2）写出批发该种水果的资金金额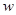（元）与批发量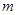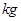（）之间的函数关系式；在图中的坐标系中画出该函数图象；指出金额在什么范围内，以同样的资金可以批发到较多数量的该种水果．
粤公网安备 44130202000953号