如图，已知AM∥BN，AC平分∠MAB，BC平分∠NBA。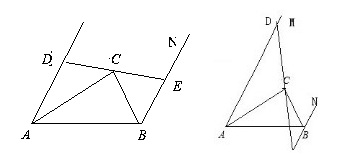
（1）过点C作直线DE，分别交AM、BN于点D、E，则AB、AD、BE三条线的长度之间存在何种等量关系？请直接写出关系式 。
（2）如图，若将直线DE绕点C转动，使DE与AM交于点D，与NB的延长线交于点E，则AB、AD、BE三条线的长度之间存在何种等量关系？请你给出结论并加以证明。
相关试题
为圆心，大圆的弦
交小圆于
、
两点．
=
．
时，求代数式
的值．
与
均是等边三角形，连接BE、CD．请在图中找出一条与
长度相等的线段，并证明你的结论．
．
相关知识点
推荐套卷
如图，已知AM∥BN，AC平分∠MAB，BC平分∠NBA。
（1）过点C作直线DE，分别交AM、BN于点D、E，则AB、AD、BE三条线的长度之间存在何种等量关系？请直接写出关系式 。
（2）如图，若将直线DE绕点C转动，使DE与AM交于点D，与NB的延长线交于点E，则AB、AD、BE三条线的长度之间存在何种等量关系？请你给出结论并加以证明。
粤公网安备 44130202000953号