如图1,点A在x轴上,点D在y轴上,以OA、AD为边分别作等边△OAC和等边△ADE,若D(0,4),A(2,0).
(1)若∠DAC=10°,求CE的长和∠AEC的度数.
(2)如图2,若点P为x轴正半轴上一动点,点P在点A的右边,连PC,以PC为边在第一象限作等边△PCM,延长MA交y轴于N,当点P运动时.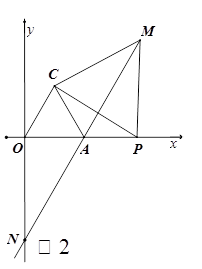
①∠ANO的值是否发生变化?若不变,求其值,若变化,请说明理由.
②AM-AP的值是否发生变化?若不变,求其值,若变化,请说明理由.
相关知识点
推荐套卷
 ,(x、y为正整数)∴
,(x、y为正整数)∴ 则有0<x<6.又
则有0<x<6.又 为正整数,则
为正整数,则 为正整数.
为正整数. .
.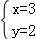
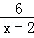 为自然数,则满足条件的x值有 个;
为自然数,则满足条件的x值有 个;
 粤公网安备 44130202000953号
粤公网安备 44130202000953号