已知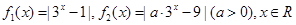
,
且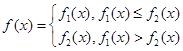
.
（Ⅰ）当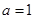
时,求
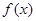在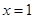
处的切线方程；
（Ⅱ）当
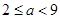时,设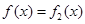
所对应的自变量取值区间的长度为
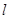（闭区间
的长度定义为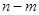
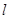）,试求的最大值；
（Ⅲ）是否存在这样的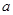
，使得当
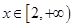时,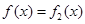?若存在,求出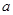的取值范围；若不存在，请说明理由.
相关试题
中，内角
的对边分别为
，且
．
的大小；
，求
中，内角
、
、
的对边分别为
、
、
，且
.
，
，求
.
和
的值；
，求
的值.
。
是第一象限角，且
。求
的值；
成立的x的取值集合。推荐套卷
已知,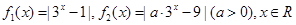
且.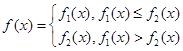
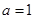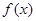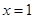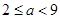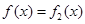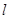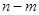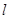（Ⅰ）当时,求在处的切线方程；（Ⅱ）当时,设所对应的自变量取值区间的长度为（闭区间的长度定义为）,试求的最大值；
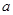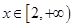（Ⅲ）是否存在这样的，使得当时,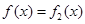?若存在,求出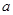的取值范围；若不存在，请说明理由.
粤公网安备 44130202000953号